Sudoku Tricks: Ghosting, RC Counting, Tagging, and Line Checking

by Kevin Rush (guest author)

Sudoku Tricks: Solving a Medium Puzzle

Welcome to Part 2. These Sudoku instruction will not be as in-depth as the Easy Instructions, because you will use the same techniques of "Checking for 1 through 9" and "Checking for one missing number in each Row, Column, and Quadrant" as in the Easy Instructions.

So in this guide I will just use the Q (Quadrant), R (Row), or C (Column) abbreviations and numbers to show where numbers go. Examples: Saying that a 4 goes in "Q5-7" means a 4 is entered in the 7th Square in Quadrant 5; "R8" means Row 8; and "C2" means Column 2.

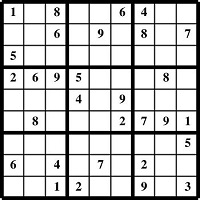
Below is the sample puzzle we will be solving. Grab a pencil, and print the Medium Sudoku Sample (page 2) of the Sudoku Puzzle Samples document so you can follow along and fill in the puzzle as we go.

Go ahead and perform the "Check for 1 Through 9" technique on this puzzle. Did you notice that no numbers are revealed going through the 1 through 9 check? No worries. Let me show you "Ghosting", the first Sudoku trick we will use to get started in this puzzle.

Sudoku Trick #1: Ghosting

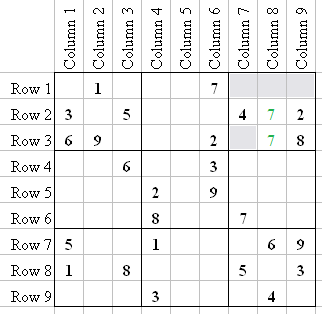
This takes a little practice, but notice Q3 and the fact that 7 can only possibly go in two squares, Q3-5 or Q3-8. I have illustrated these 7's in the image above. Knowing that the 7 for C8 has to be in Q3 is a Sudoku trick called "Ghosting", and it reveals something in Q9.

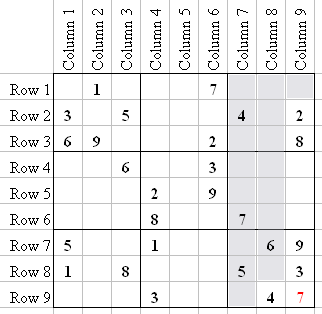
So now we know the only place a 7 can go in Q9 is Q9-9. Looking at the 1's in R7 and R8, we now know that 1 can only go in Q9-7. That leaves only 2 and 8 in Q9. Well, the 8 can't go in Q9-5 because R8 has an 8 at Q7-6. So 2 must go in Q9-5, and the 8 goes in Q9-1.

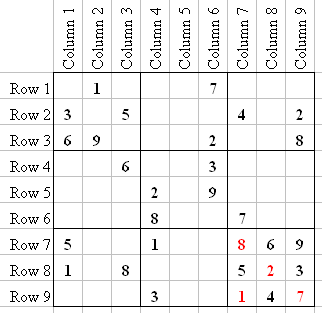
There is another such Ghost in Q3 like the 7, and I will show it to you. It does not help with another number right now, but it will later. I just want to show you, so you can get used to looking for them.

Notice that there are only two squares a 6 can go in Q3: Q3-1 and Q3-3. That means that in Q2, the 6 can only go in R2. Remembering that will help later; but for now I just want you to notice it.

Sudoku Trick #2: Row/Column Counting

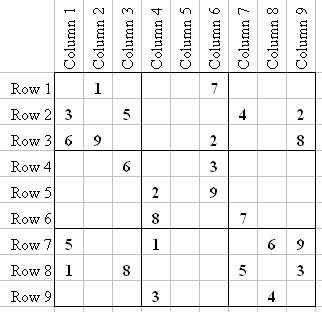
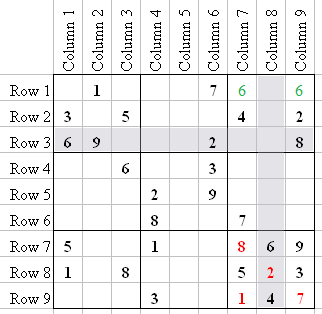
Now look at Q8-3 in the above image. Notice that in R7 you have numbers 1, 5, 6, 8, and 9, and in C6 you have 2, 3 (the 3 is also already in Q8), 7, and 9 (the 9 is also in R7).

But did you notice that every number is there except 4? Given any Row and Column, the square where they intersect is obviously a single number; and if all numbers 1 through 9, except one, appear in the rest of the squares of that Row and Column, then the missing number itself must be located at that intersection. This Sudoku trick can be referred to as Row/Column Counting (or RC Counting).

After we enter the 4 in Q8-3, look to see what numbers are missing in Q8-6 (that is, the square at the intersection of R8 and C6). Did you notice that the only number missing from all the numbers in R8 and C6 put together is 6?

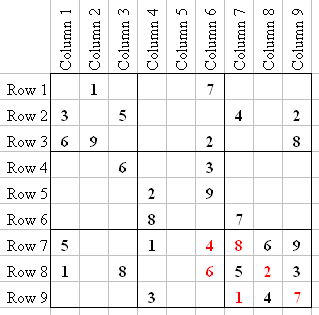
Once again, in this case the number where that Row and Column cross each other is the only number between 1 and 9 that we didn't see already in either Row or Column.

Sudoku Trick #3: Tagging

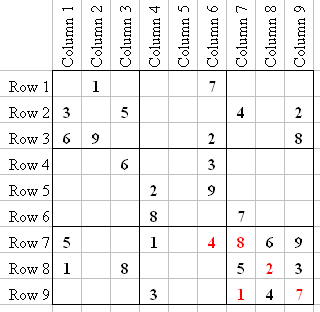
Let's stay in Q8. I want to show you something else that will help you solve difficult puzzles. Notice that R7 and R8 already have a 5 and 8. So the only places a 5 and 8 can go in R9 are Q8-8 and Q8-9. Place little "5" and "8" number markers in those positions to remember that.

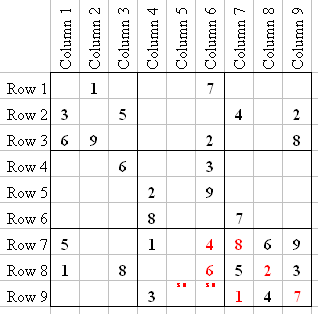
The small 5 and 8 in the above picture I call "Tags". That means that only the numbers in the Tag can go into those squares (you will see more of them later on). This Tagging is a very helpful Sudoku trick.

In Medium Sudoku puzzles, try not to put more than 3 Tags in a square. In Hard puzzles you can put more; in those more difficult puzzles it is not uncommon to have 5 or 6 Tags in a square.

At first glance it looks like a 2 or 9 could go into Q8-8, but knowing that a 5 and 8 can only go into those two squares eliminates the 2 and 9 from Q8-8 and Q8-9. Knowing that a 2 can't go in Q8-8, and R8 and C6 already have a 2, that only leaves Q8-2 for the 2.

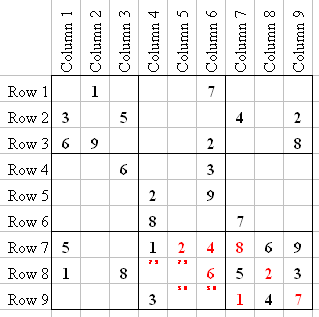
Now we Tag the last two squares in Q8 (Q8-5 and Q8-6) with a 7 and 9. So now there is only one number left in R8, and it is a 4 which goes in Q7-5.

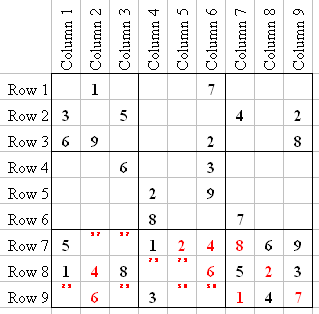
R7 is now only missing two numbers, so we Tag them with 3 and 7 (at Q7-2 and Q7-3). The 6 can only go into Q7-8, because of the 6 in C1 and C3; which means that only 2 and 9 can go into Q7-7 and Q7-9, so we Tag them.

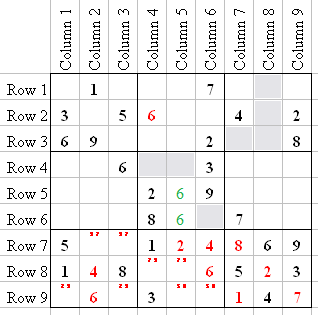
Now let's look at Q5. The only places a 6 could go (Ghosts) are Q5-5 and Q5-8. That information does not help us with Q5, but remember when I showed you the Ghosted 6 in Q3 (Q3-1 and Q3-3)? Now it helps us with Q2. The Ghosted 6's in Q3 and Q5 taken together now show us that the 6 in Q2 has to go in Q2-4.

Let's also look at Q3-7, which is the intersection of R3 and C7. Count the numbers that appear in R3 and C7 at this point, and you will see that just the 3 is missing (this is the RC Counting trick again). So 3 goes in Q3-7.

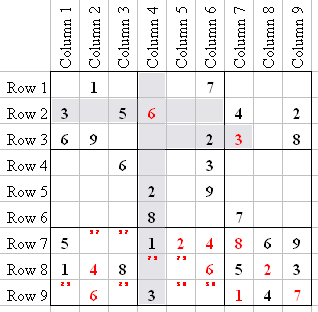
After entering the 3 in Q3-7, we now know that Q2-2 has to be a 3. Q6-1 has to be a 2, because of the 2 in R5, C8, and C9.

Sudoku Trick #4: Line Checking

Let's look at Q4. It looks like there are three squares where a 2 can go (Q4-7, Q4-8, and Q4-9). But there is really only one square. Let me explain how I know that.

If you "Line Check" C2, you will see that a 2 can't go in C2 at R2, R4, R5, or R7, because there is already a 2 in each of those Rows. So Q4-8 is the only square for a 2 in C2. This Sudoku trick is called Line Checking, and you can Line Check a Row or Column.

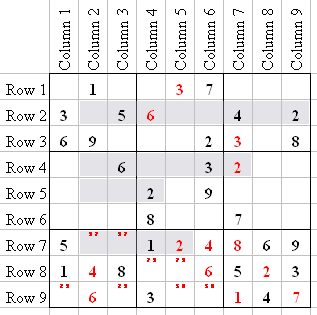
We can use Line Check again for C7. There are only two numbers missing in C7: 6 and 9. R5 already has a 9, so Q6-4 has to be a 6. So 9 is the last number in C7, at Q3-1.

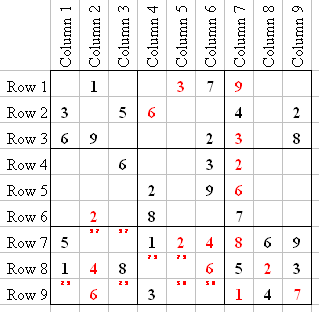
Because we entered a 9 in Q3-1, and remembering the Ghosted 6 in Q3, we now know that Q3-3 has to be a 6. Q3 is now only missing 1, 5, and 7, but R1 already has a 1 and 7 so 5 is the only number that can go into Q3-2, leaving 1 and 7 Tagged in Q3.

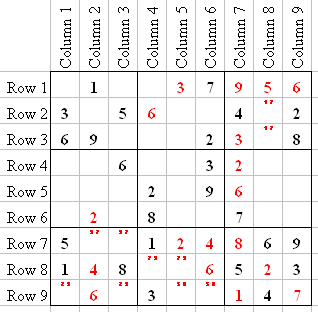
R1 is now missing numbers 2, 4, and 8. If you look at C4, you will see that it already has a 2 and 8, so Q2-1 has to be a 4. Leaving 2 and 8 for R1... but if you look, you will see that C3 already has an 8, so Q1-3 has to be a 2, leaving an 8 in Q1-1.

Now let's look at Q1. There are only two numbers missing: 4 and 7. R2 already has a 4, so Q1-9 is a 4 and Q1-5 is a 7.

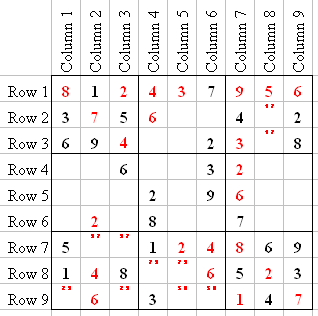
Now I will show you the advantage of the "Tagging" Sudoku trick. Since we put a 7 in Q1-5, we now know that Q3-5 has to be a 1, and Q3-8 has to be a 7.

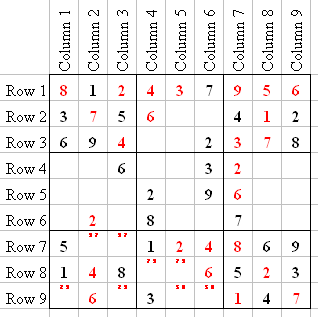
R2 is only missing 8 and 9. C6 already has a 9, so Q2-6 has to be 8, leaving Q2-5 a 9. R3 is missing 1 and 5. C4 already has a 1, so Q2-7 has to be a 5, and Q2-8 will be a 1.

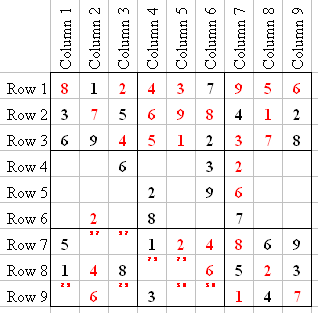
R8 is Tagged with 7 and 9. We entered a 9 in C5 at Q2-5, so Q8-5 has to be a 7, and Q8-4 has to be a 9. R9 is "Tagged" with 5 and 8. We entered an 8 in C6 at Q2-6, so Q8-9 has to be a 5, and Q8-8 is an 8.

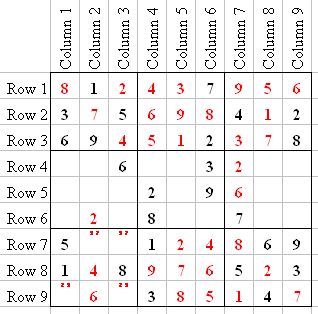
Now C4 and C6 are missing only one number. C4 is missing a 7, and C6 is missing a 1. In R7 we Tagged 3 and 7. We entered a 7 in Q1-5, so Q7-2 has to be a 3, and Q7-3 is a 7. In R9 we Tagged 2 and 9. We entered a 2 in Q1-3, so Q7-9 has to be a 9, and Q7-7 is a 2.

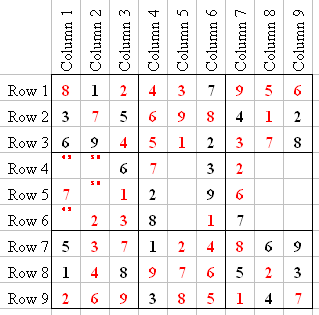
If we Line Check C1, we will see that 7 can only go into Q4-4, and C3 can only have a 1 at Q4-6, leaving a 3 in C3 at Q4-9. We can Tag C1 with 4 and 9 and C2 with 5 and 8. If we Line Check C5, we will see that 6 can only go into Q5-8, leaving 4 and 5 Tagged in C5.

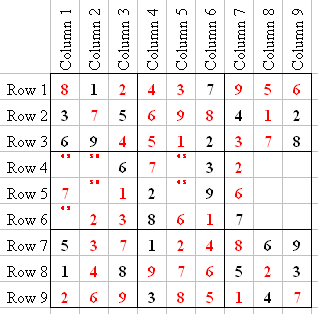
If we Line Check C8, we see that Q6-5 has to be a 3, Q6-2 has to be an 8, and the last number in C8 is a 9. Now if we look at the Tagged numbers in Q4, we now know that Q4-7 is 4, Q4-1 is 9, Q4-2 is 5, and Q4-5 is 8. That only leaves us with 3 numbers.

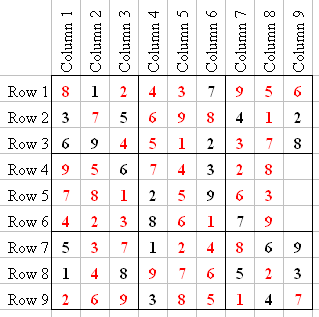
If we Line Check C9 we will see that Q6-3 is 1, Q6-6 is 4, and Q6-9 is 5.

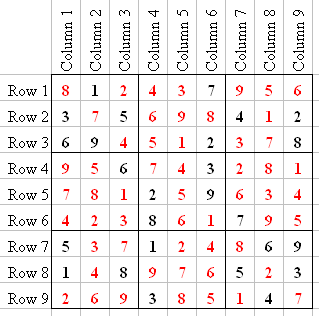
So what started out as a difficult-looking puzzle was solved pretty easily. All we needed to do was find a "Ghost" in a Quadrant, like the 7 and 6 in Q3 at the beginning of these instructions.

After you get used to finding Ghost numbers, the RC Counting, Tagging, and Line Checking techniques will not seem as difficult.

Once you are comfortable solving Medium puzzles, study the Hard Instructions, where I will show you more tricks to Ghosting, RC Counting, Tagging, and Line Checking.

~ Kevin Rush

Published: 04/10/2020
Last Updated: 06/11/2020